the world in a different light
This deck of slides are the ones I will be using for the Symposium on “Leveraging Technology for Engaging and Effective Learning” at the Singapore International Science Teachers’ Conference (SISTC) 2024 on Day 2 of the Conference (20 November). Feel free to download for your reference.
The simulation below allows students to practise calculating potential differences and currents of a slightly complex circuit, involving three different modes that can be toggled by clicking on the switch.
Link: https://www.geogebra.org/m/jkckp9pr
When resistors \( R_1 \) and \( R_2 \) are connected in series, the total resistance is simply the sum of the individual resistances:
\[ R_{\text{total}} = R_1 + R_2 \]
The current \( I \) through the circuit is given by Ohm’s Law:
\[ I = \frac{V_{\text{total}}}{R_{\text{total}}} = \frac{V_{\text{total}}}{R_1 + R_2} \]
where \( V_{\text{total}} \) is the total potential difference supplied by the source.
The potential difference across each resistor can be calculated using:
\[ V_1 = I \cdot R_1, \quad V_2 = I \cdot R_2 \]
In this mode, resistors \( R_1 \) and \( R_3 \) are in parallel, and \( R_2 \) is in series with the combination. First, calculate the equivalent resistance of the parallel combination:
\[ \frac{1}{R_{\text{parallel}}} = \frac{1}{R_1} + \frac{1}{R_3} \]
Thus, the total resistance is:
\[ R_{\text{total}} = R_{\text{parallel}} + R_2 \]
The current through the circuit is:
\[ I = \frac{V_{\text{total}}}{R_{\text{total}}} \]
The potential difference across \( R_2 \) is:
\[ V_2 = I \cdot R_2 \]
Since \( R_1 \) and \( R_3 \) are in parallel, they share the same potential difference:
\[ V_1 = V_3 = V_{\text{total}} – V_2 \]
The current through each parallel resistor can be found using Ohm’s Law:
\[ I_1 = \frac{V_1}{R_1}, \quad I_3 = \frac{V_3}{R_3} \]
Here, resistors \( R_1 \) and \( R_2 \) are connected in series, and the combination is in parallel with \( R_3 \). First, calculate the resistance of the series combination:
\[ R_{\text{series}} = R_1 + R_2 \]
Then, find the total resistance of the parallel combination:
\[ \frac{1}{R_{\text{total}}} = \frac{1}{R_{\text{series}}} + \frac{1}{R_3} \]
The total current is:
\[ I = \frac{V_{\text{total}}}{R_{\text{total}}} \]
The voltage across the parallel combination is the same for both branches:
\[ V_1 + V_2 = V_3 = V_{\text{total}} \]
The current through \( R_3 \) is:
\[ I_3 = \frac{V_3}{R_3} \]
The current through \( R_1 \) and \( R_2 \), which are in series, is the same:
\[ I_{\text{series}} = \frac{V_{\text{total}}}{R_1 + R_2} \]
The voltage across each series resistor is:
\[ V_1 = I_{\text{series}} \cdot R_1, \quad V_2 = I_{\text{series}} \cdot R_2 \]
I modified an existing simulation to demonstrate how the displacement of particles along a longitudinal wave can be represented in graphical form.
Essentially, one would have to determine for each particle, its displacement from the equilibrium position and its corresponding position along the wave’s direction. On the graph, positive displacement indicates movement in one direction (e.g., to the right), while negative displacement indicates movement in the opposite direction (e.g., to the left).
For the full view, go to https://www.geogebra.org/m/kq3e2qjk
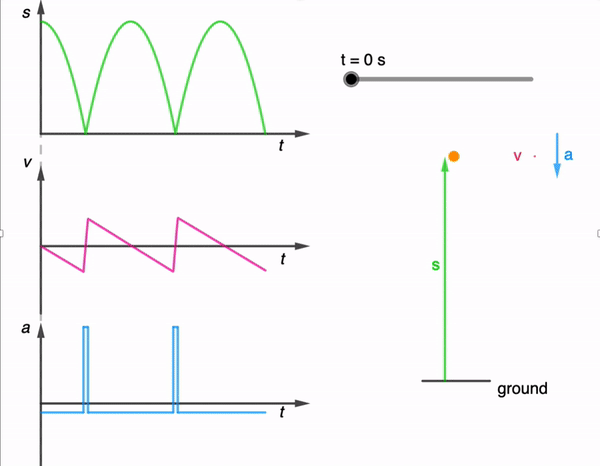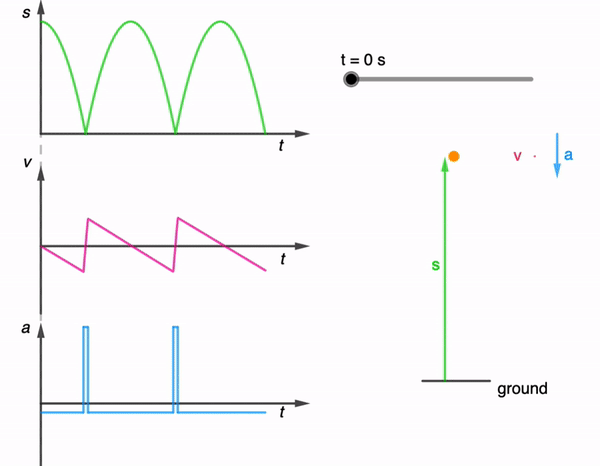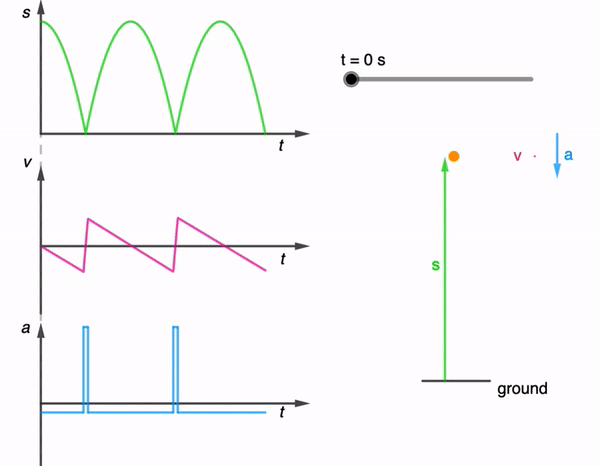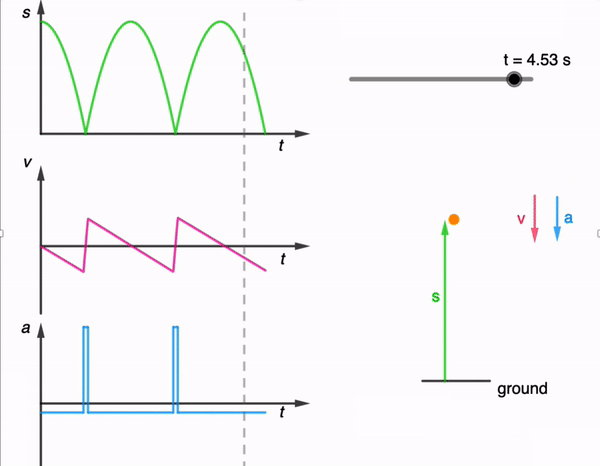
While I have shared a simulation of a bouncing ball made using Glowscript before, I felt that one made using GeoGebra is necessary for a more comprehensive library.
It took a while due to the need to adjust the equations used based on the position of the graphs, but here it is: https://www.geogebra.org/m/dfb53dps
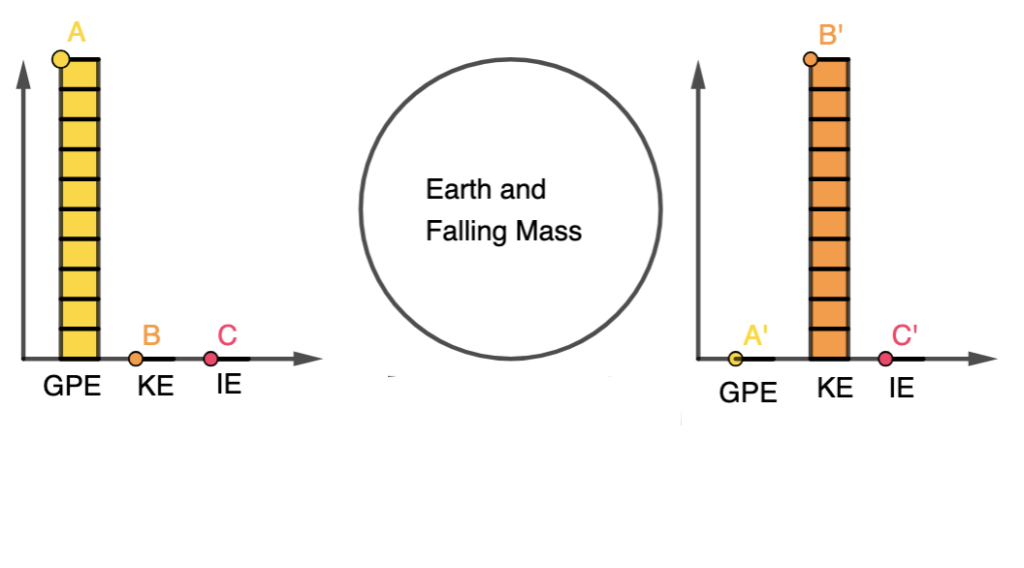
The kinematics of a bouncing ball can be explained by considering the dynamics and forces involved in its motion. In this simulation, air resistance is assumed negligible. When a ball is dropped from a certain height and bounces off the ground, several key principles of physics come into play. Let’s break down the process step by step:
Free Fall: When the ball is released, it enters a state of free fall. During free fall, the only force acting on the ball is gravity. This force is directed downward and can be described by W = mg
W is the gravitational force.
m is the mass of the ball.
g is the acceleration due to gravity (approximately 9.81 m/s² near the surface of the Earth).
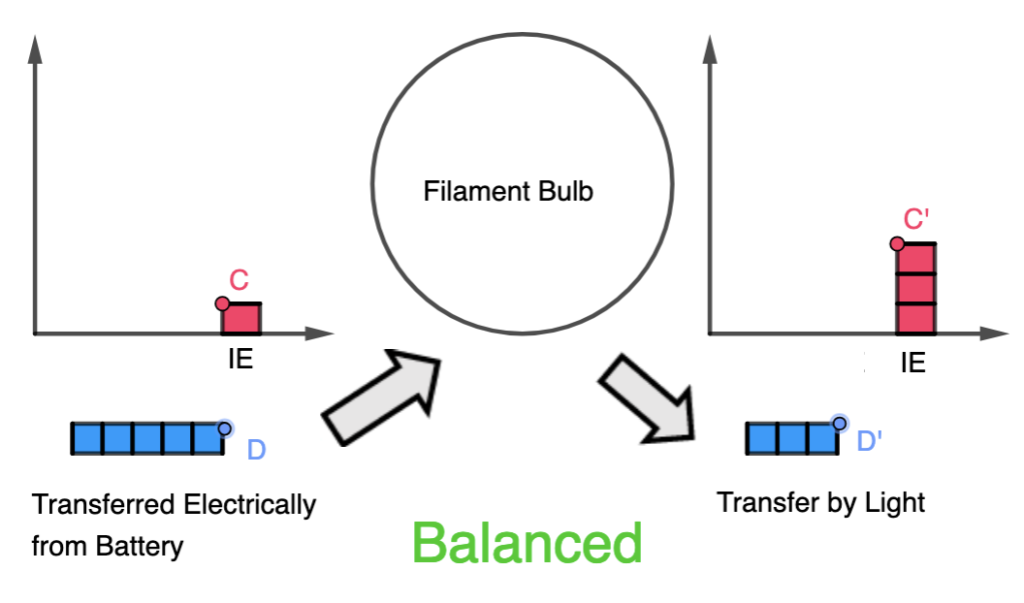
Impact with the Ground and Bounce: When the ball reaches the ground, it experiences a force due to the collision with the surface. This force is an example of a contact force and much larger than the gravitational force. This force depends on the elasticity of the ball and the surface it bounces off.
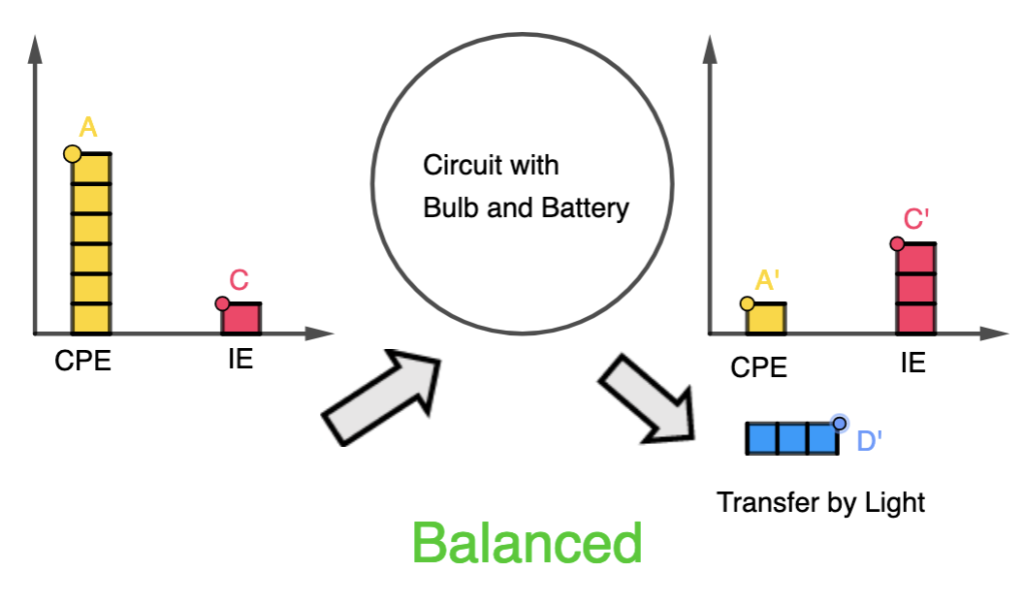
During the collision with the ground, the ball’s momentum changes rapidly. If the ball and the ground are both ideal elastic materials, the ball will bounce back with the same speed it had just before impact. In reality, some energy is lost during the collision, causing the bounce to be less than perfectly elastic. This simulation assumes elastic collisions.
Post-Bounce Motion: After the bounce, the ball starts moving upward. Gravity acts on it as it ascends, decelerating its motion until it reaches its peak height.
Second Descent: The ball then starts descending again, experiencing the force of gravity pulling it back down towards the ground.
This process continues with each bounce. In practice, with each bounce, some energy is lost due to the non-ideal nature of the collision and other dissipative forces like air resistance. As a result, each bounce is typically lower than the previous one until the ball eventually comes to rest. However, for simplicity, the simulation assumes no energy is lost during the collision and to dissipative forces.
An animated gif file is included here for use in powerpoint slides:
Direct link: https://www.geogebra.org/m/u2m3gnzj
The above is a GeoGebra applet that can be customised for any energy problem. Simply make a copy of it and change the values or labels as needed. This can be integrated into either GeoGebra Classroom or Google Classroom (as a GeoGebra assignment) and the teacher can then monitor every student’s attempt at interpreting the energy changes in the problem. The teacher can also choose different extents of scaffolding, e.g. provide the initial or final states and ask students to fill in the rest.
An LOL diagram is a tool used to visualize and analyze the conservation of energy in physical systems. “LOL” does not stand for anything meaningful. Rather, they just form the shapes of the two sets of axes and the circle in between. They help clarify which objects or components are included in the energy system being considered and how energy is transferred or transformed within that system.
In LOL diagrams:
When performing calculations involving the initial and final energy states, the energy transferred into the system is added to the initial energy state while the energy transferred out of the system is added to the final energy state. The sums must be equal. In other words,
Initial energy stores + Energy transferred into system = Final energy stores + Energy transferred out of system
Here’s a breakdown of how LOL diagrams are used, using an example of a falling mass:
LOL diagrams illustrate that energy within the system is conserved, meaning the total energy in the system remains constant.
External work (work done by forces outside the defined system) may impact the system’s energy, but internal work (work done within the defined system) does not change the total energy of the system.
The mathematical representation of the above problem will then simply be:
GPE = KE
$mgh = \dfrac{1}{2}mv^2$
This problem seems a bit trivial. Since LOL diagrams are a visual tool to help students and scientists analyze energy transformations and conservation, they can be used for making it easier to set up and solve conservation of energy equations in problems of greater complexity.
It is also important to note that the choice of the object (or system) of interest will result in different LOL diagrams for the same phenomenon.
For example, consider a filament bulb in a circuit with a battery. The system at room temperature also has some energy in the internal store (or internal energy, which consists of the kinetic and potential energies of the particles in the system).
When considering the filament as the object of interest, when energy is transferred electrically from the battery, part of it is transferred by light from the bulb to the surroundings and another part is added to the internal store, as it heats up the filament light.
On the other hand, when considering the circuit as the whole, the chemical potential store of the battery is included in the initial energy state of the system. Hence, there is no additional energy transfer into the system but the energy transfer output is still the same.
Here’s a video that demonstrates how the editing process is done, in a little more than one minute!
The final product is here.
My third applet today is a self-assessment tool for students to practise calculations with Snell’s Law, i.e. $n_1 \sin{\theta_1} = n_2 \sin{\theta_2}$.
The direct link to the applet is https://www.geogebra.org/m/fhmmuhbg
Snell’s law, also known as the law of refraction, describes how light waves change direction as they pass from one medium to another with different refractive indices. It states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant for a given pair of media. This law is fundamental in understanding the bending of light when it moves between materials of different optical densities, such as when light passes from air to water, resulting in phenomena like the bending of a pencil in a glass of water.
When light travels from a medium with higher optical density to a medium with lower optical density,
When light travels from a medium with lower optical density to a medium with higher optical density,
When light travels from a medium with a higher refractive index to a medium with a lower refractive index and strikes the interface at an angle of incidence greater than the critical angle, total internal reflection occurs. At this critical angle, the light is entirely reflected back into the higher refractive index medium, with no refraction into the second medium, resulting in the complete internal reflection of the light. This phenomenon is crucial in various applications, such as optical fiber communications and the brilliance of gemstones like diamonds.
Update on 27 Jul 2023: I improved on the rather unpolished applet to adjust the calculations for the object when it is below the boundary between the two media. Also added was an indication for when total internal reflection takes place.