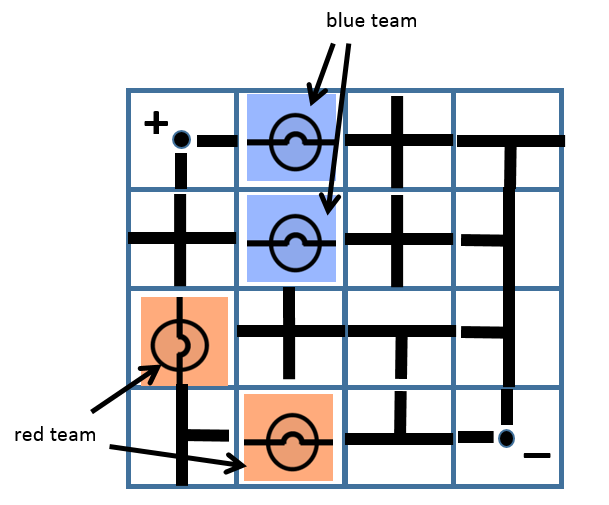
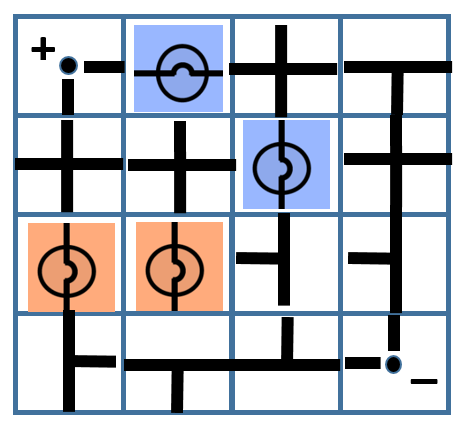
I had previously shared about this physical board game that I designed to teach electricity concepts. Now, with ChatGPT’s help, I have managed to produce a simple implementation of the board game so that there is no need to print and cut out the pieces anymore.
However, the game is still unable to detect if the light bulb will light up and automatically change the image colour or add the scores. That will require further complex programming due to the many possible outcomes for this game.
https://physicstjc.github.io/sls/delight/index.html
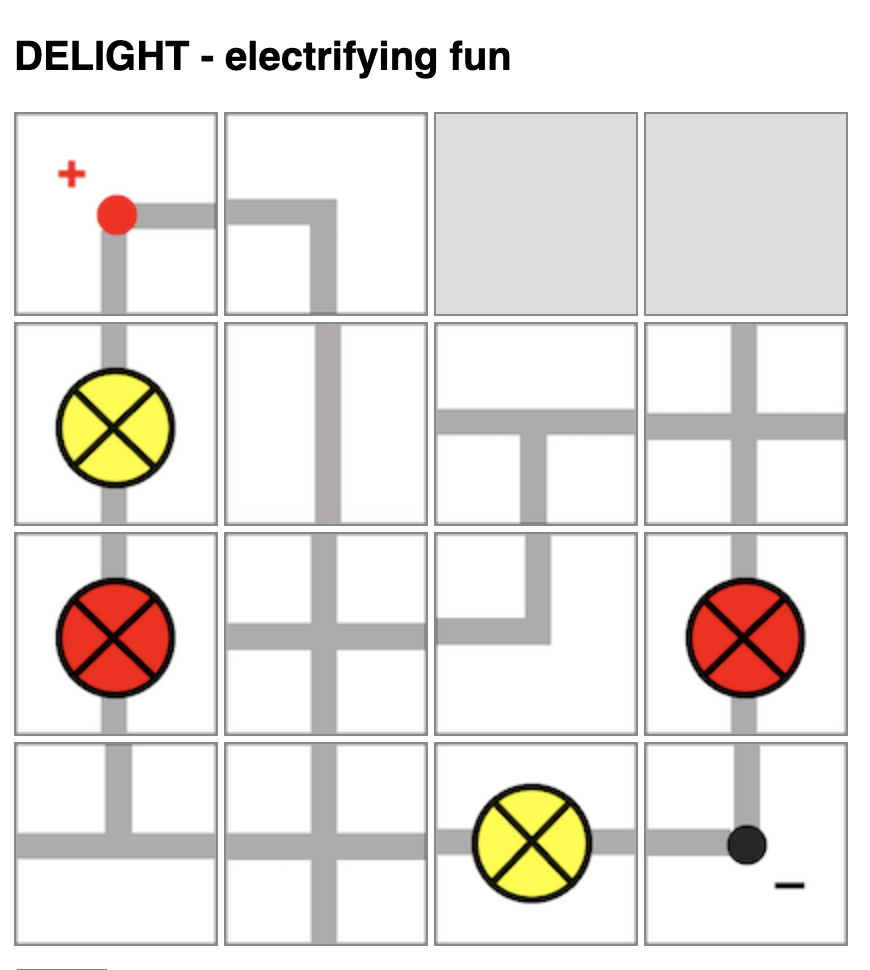
The rules of the game are as such:
- Players will take turns to connect their own bulbs to the terminals while trying to sabotage their opponent’s bulbs.
- Players will take turns to place one piece on the 4-by-4 game board by clicking to select the electrical component and clicking on the square on the board to place it.
- Upon placing the piece, the player can also turn that piece in any orientation (by clicking on it) within the same turn.
- Players can choose to use up to two turns at any point in the game to rotate any piece that had been placed by any player.
- In other words, each player has 9 turns: 7 placement turns and 2 rotation turns.
At lower levels, students can compete to see who has the most lit bulbs. However, they will need to be able to identify which light bulbs are lit. Do watch out for short-circuits.
At higher levels, students can compete to see whose light bulbs has the most total electrical power, with some calculations involved.