In recent years, AI tools like DALL-E and MidJourney have gained popularity for generating stunning, artistic images. However, when it comes to creating scientific illustrations, particularly for exams, we need accuracy, clarity, and precision. This is where LaTeX, a document preparation system widely used in academia, shines. Combined with the intelligence of ChatGPT, LaTeX can produce exactly the images you need without the artistic flair or ambiguity that tools like DALL-E might introduce.
The process of generating science exam images using ChatGPT and LaTeX is straightforward:
- Describe the Diagram: You begin by providing a detailed description of the diagram or scientific illustration you need. For example, “Generate a diagram using Latex showing a free-body diagram of a block on an inclined plane with friction.”
- ChatGPT Generates LaTeX Code: Based on your description, ChatGPT can generate the appropriate LaTeX code, using packages like TikZ or PGFPlots to create the required scientific diagram. The output might look like this:
\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}
% Inclined plane
\draw[thick] (0,0) -- (4,2);
\draw[thick] (0,0) -- (4,0);
% Block
\draw[fill=gray] (2,1) rectangle (2.5,1.5);
% Forces
\draw[->,thick] (2.25,1.25) -- (2.25,2.25) node[above] {Normal Force};
\draw[->,thick] (2.25,1.25) -- (2.25,0.25) node[below] {Weight};
\draw[->,thick] (2.25,1.25) -- (3.25,1.25) node[right] {Friction};
\end{tikzpicture}
\end{document} - Compile the LaTeX Code: Once the code is generated, you can compile it using any LaTeX editor (such as Overleaf or a local LaTeX distribution).
- Check for Errors: The diagram is unlikely to look perfect in the first iteration. For example, the above code gives the following:

- Edit: You can either instruct ChatGPT to modify specific sections of the diagram or make the changes yourself. After 3 more iterations, for example, ChatGPT produced the following codes:
\begin{tikzpicture}
% Inclined plane
\draw[thick] (0,0) -- (4,2);
\draw[thick] (0,0) -- (4,0);
% Block (rotated to match the slope)
\draw[fill=gray, rotate around={26.565:(2.25,1.25)}] (2,1) rectangle (2.5,1.5);
% Forces (adjusted for friction up the slope)
% Normal Force (perpendicular to the slope)
\draw[->,thick] (2.25,1.25) -- ++(-0.447,0.894) node[above left] {Normal Force};
% Weight (straight down)
\draw[->,thick] (2.25,1.25) -- (2.25,0.25) node[below] {Weight};
% Friction (along the slope, now pointing up the incline)
\draw[->,thick] (2.25,1.25) -- ++(0.894,0.447) node[above right] {Friction};
\end{tikzpicture} - This is the output image:

- Integrate into Teaching Materials: Once you are satisfied with the output, the compiled image can then be saved as a PDF, PNG, or any other image format and directly embedded into your exam materials.
The following are similar images made using the same workflow and their corresponding codes, which I made changes to manually instead as it was faster for me once I became familiar with the coordinate-system based drawing method.
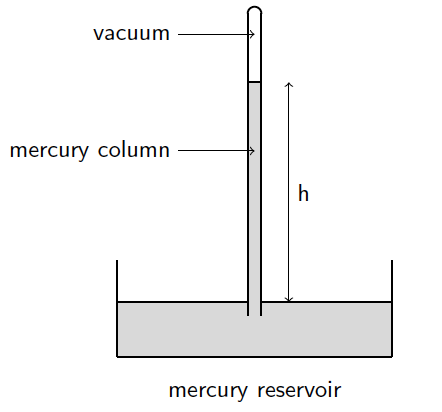
\begin{tikzpicture}
% Draw the base container (mercury reservoir)
\draw[draw=none, fill=gray!30] (-2,-0.2) rectangle (2,-1);
\draw[thick] (-2,-1) -- (-2,0.4);
\draw[thick] (2,-1) -- (2,0.4);
\draw[thick] (-2,-1) -- (2,-1);
\draw[thick] (-2,-0.2) -- (-0.1,-0.2);
\draw[thick] (0.1,-0.2) -- (2,-0.2);
% Mercury inside the tube
\draw[draw=none, fill=gray!30] (-0.1,3) -- (-0.1,-0.3) -- (0.1,-0.3) -- (0.1,3) -- cycle;
\draw[thick] (-0.1,3) -- (0.1,3);
% Draw the glass tube
\draw[thick] (0.1,4) -- (0.1,-0.4); % Tube
\draw[thick] (-0.1,4) -- (-0.1,-0.4); % Tube
% Label for the mercury level
\draw[<-] (0,2) -- (-1.1,2) node[left]{mercury column};
\draw[<-] (0,3.7) -- (-1.1,3.7) node[left]{vacuum};
\draw[thick] (0,4) ++(0:0.1cm) arc (0:180:0.1cm);
% Labels for height
\draw[<->] (0.5,3) -- (0.5,-0.2) node[midway,right]{h};
% Add some text labels
\node at (0,-1.5) {mercury reservoir};
\end{tikzpicture} 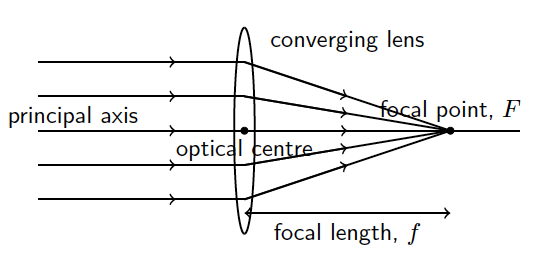
\begin{tikzpicture}
% Draw principal axis
\draw[thick] (-5,0) -- (2,0) node at (-4.5,0.2) {principal axis};
% Draw the lens
\draw[thick] (-2,-1.5) arc[start angle=270, end angle=90, x radius=0.15cm, y radius=1.5cm];
\draw[thick] (-2,1.5) arc[start angle=90, end angle=270, x radius=-0.15cm, y radius=1.5cm];
% Draw the focal points
\node at (1, 0) [above] {focal point, $F$};
\draw[fill] (1, 0) circle [radius=0.05];
\node at (-2, 0) [below] {optical centre};
\draw[fill] (-2, 0) circle [radius=0.05];
% Draw the 3 rays parallel to the principal axis (before hitting the lens)
\draw[thick] (-5,1) -- (-2,1);
\draw[thick] (-5,0.5) -- (-2,0.5);
\draw[thick] (-5,-0.5) -- (-2,-0.5);
\draw[thick] (-5,-1) -- (-2,-1);
\draw[thick, ->] (-4,1) -- (-3,1);
\draw[thick, ->] (-4,0.5) -- (-3,0.5);
\draw[thick, ->] (-4,-0.5) -- (-3,-0.5);
\draw[thick, ->] (-4,-1) -- (-3,-1);
\draw[thick, ->] (-4,0) -- (-3,0);
% Rays converging to the focal point F
\draw[thick] (-2,1) -- (1,0);
\draw[thick] (-2,0.5) -- (1,0);
\draw[thick] (-2,-0.5) -- (1,0);
\draw[thick] (-2,-1) -- (1,0);
\draw[thick, ->] (-2,1) -- (-0.5,0.5);
\draw[thick, ->] (-2,0.5) -- (-0.5,0.25);
\draw[thick, ->] (-2,0) -- (-0.5,0);
\draw[thick, ->] (-2,-0.5) -- (-0.5,-0.25);
\draw[thick, ->] (-2,-1) -- (-0.5,-0.5);
\node at (-0.5, 1.3) {converging lens};
% Focal length
\draw[thick, <->] (-2,-1.2) -- (1,-1.2);
\node at (-0.5, -1.5) {focal length, $f$};
\end{tikzpicture}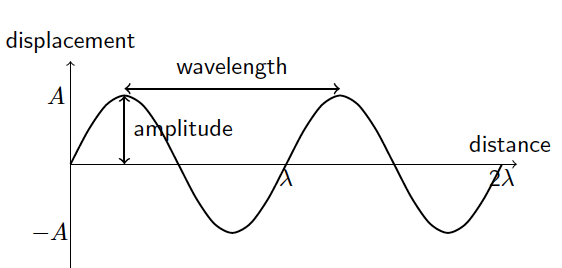
\begin{tikzpicture}
% Draw the wave
\draw[thick, domain=0:6.28, smooth, variable=\x] plot ({\x}, {sin(2*\x r)});
% Draw the x-axis
\draw[->] (0, 0) -- (6.5, 0) node at (6.4,0.3) {distance};
% Draw the y-axis
\draw[->] (0, -1.5) -- (0, 1.5) node[above] {displacement};
% Draw the amplitude arrow
\draw[<->, thick] (0.785, 0) -- (0.785, 1) node[midway, right] {amplitude};
% Draw the wavelength arrow
\draw[<->, thick] (0.785, 1.1) -- (3.925, 1.1) node at (2.355,1.4) {wavelength};
% Label the points
\node at (-0.2, 1) {$A$};
\node at (-0.3, -1) {$-A$};
\node at (3.14, -0.2) {$\lambda$};
\node at (6.28, -0.2) {2$\lambda$};
\end{tikzpicture}