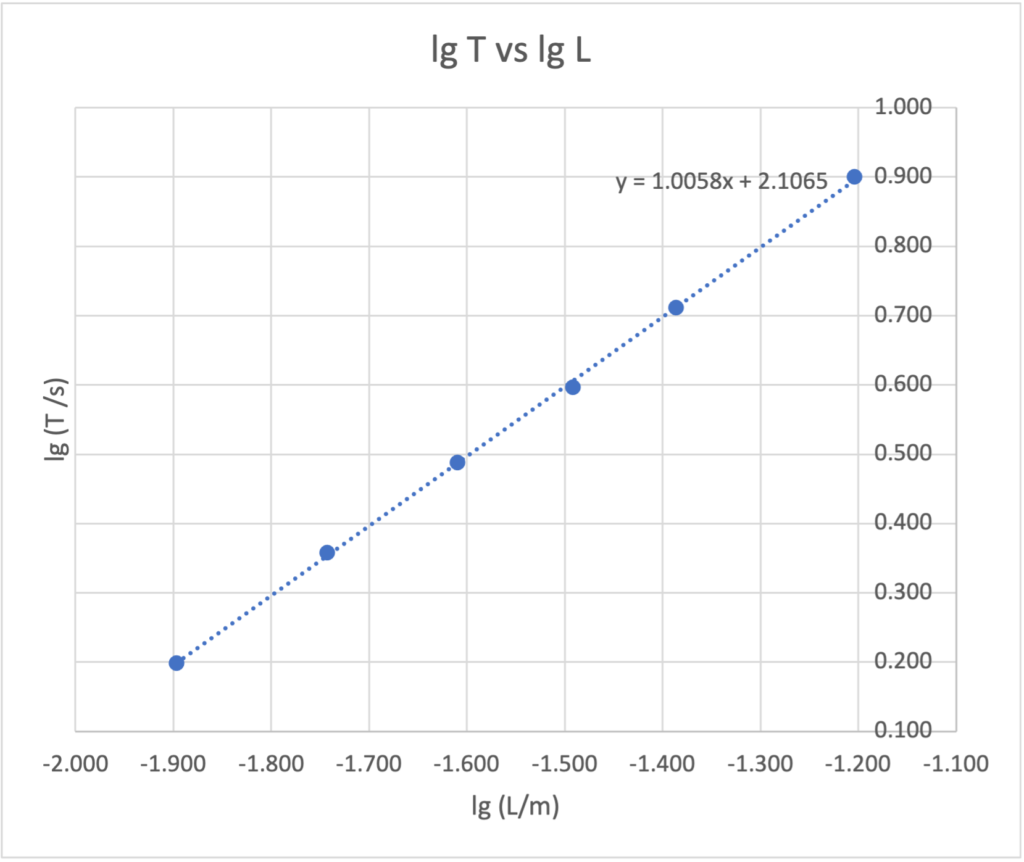
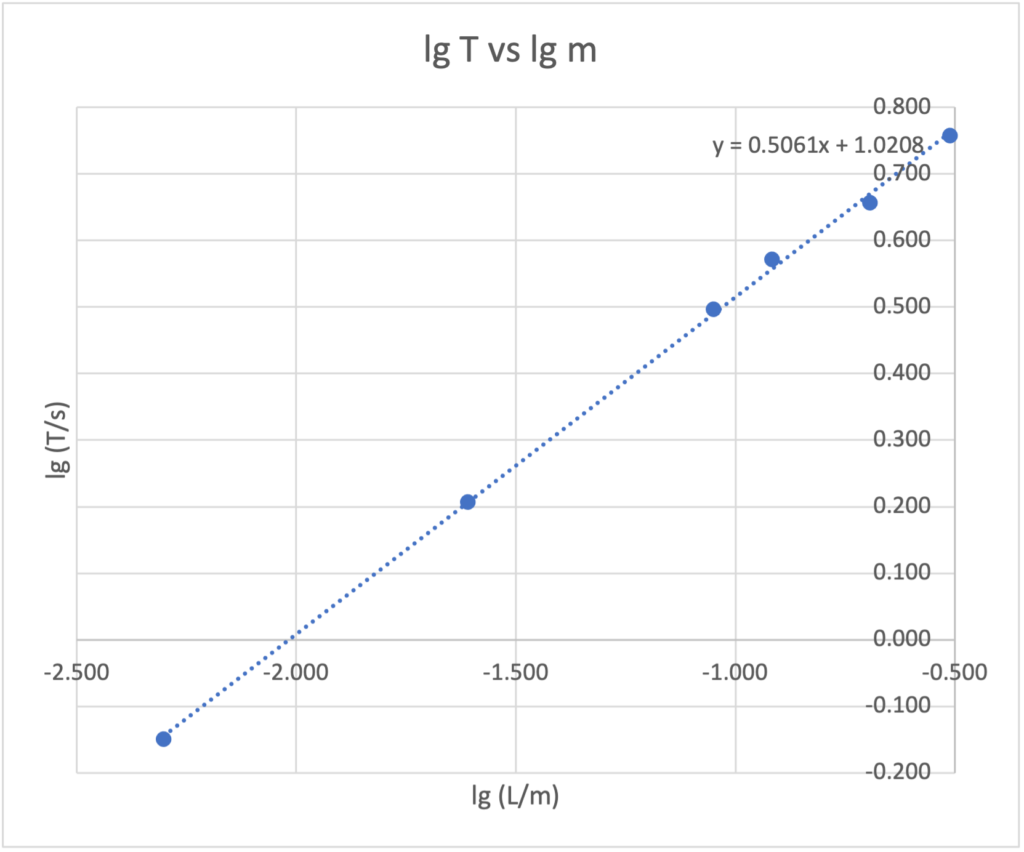
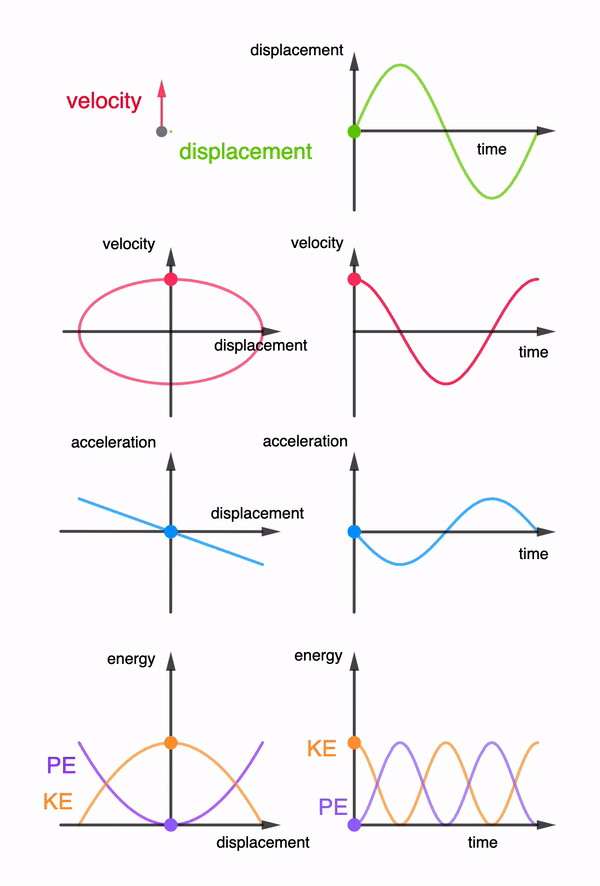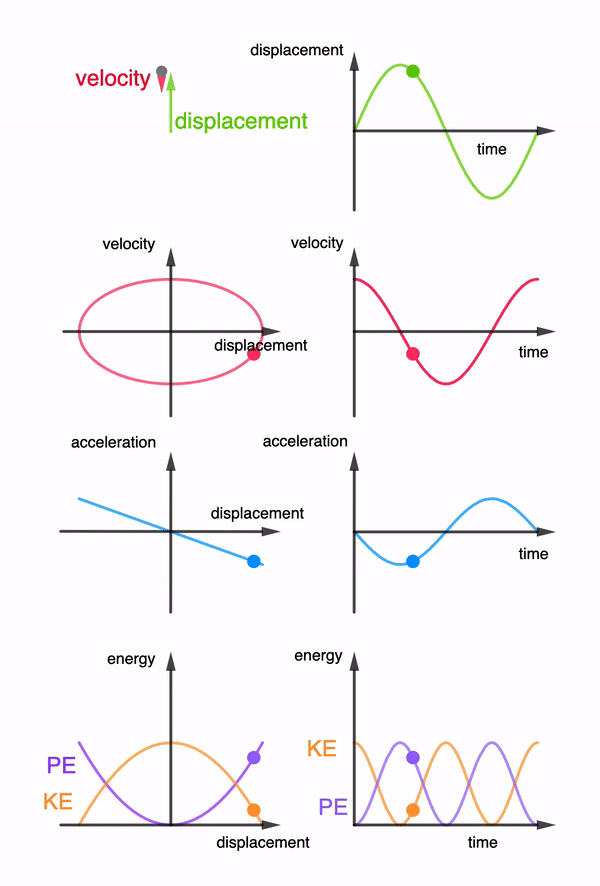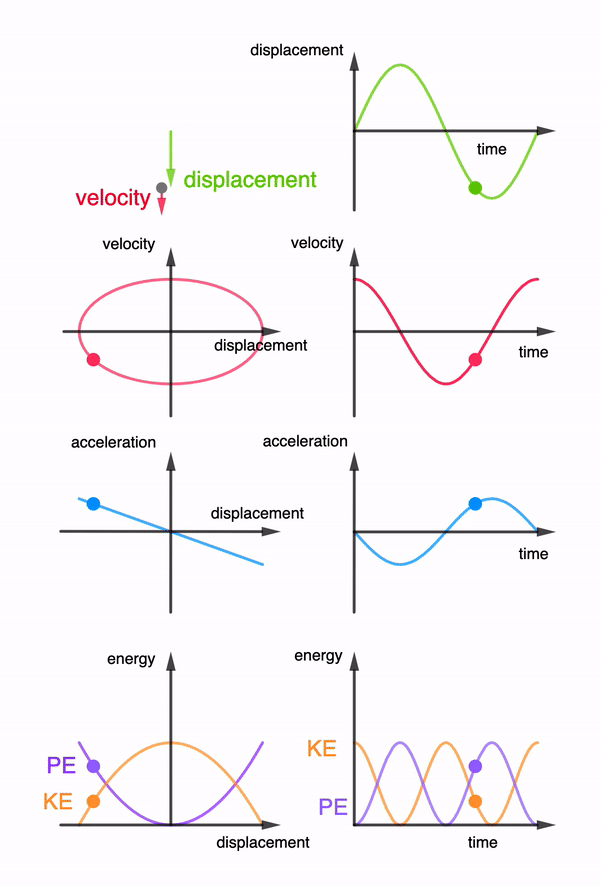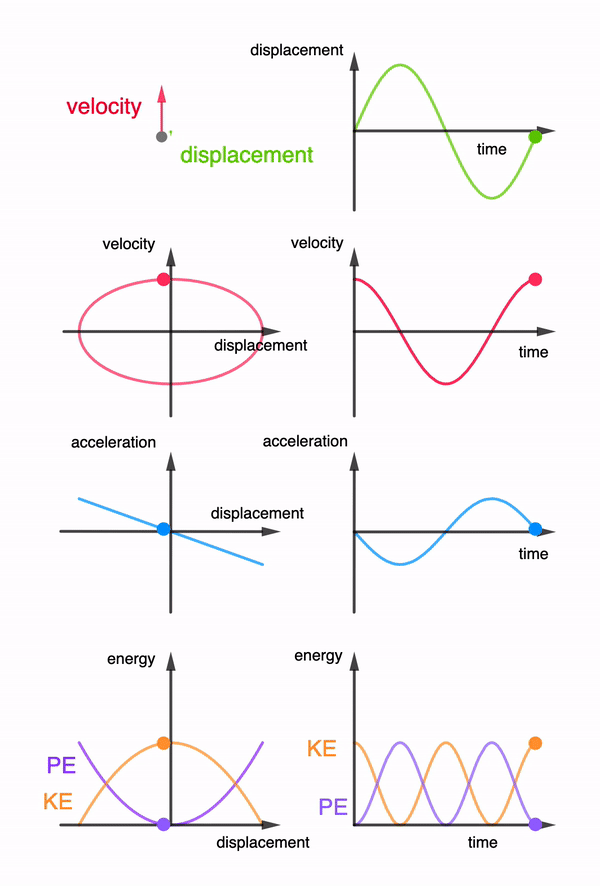
This is a common example used in the JC1 topics of Oscillations, where if one were to look at an object moving in circles from the side view, it will appear to move in simple harmonic motion. This simple 3D animation allows users to rotate the view to see exactly that. Right click and drag to rotate the view. If you are using a mobile device, use two fingers to drag.
To access the animation in full screen, visit https://www.geogebra.org/m/tsz95u6p