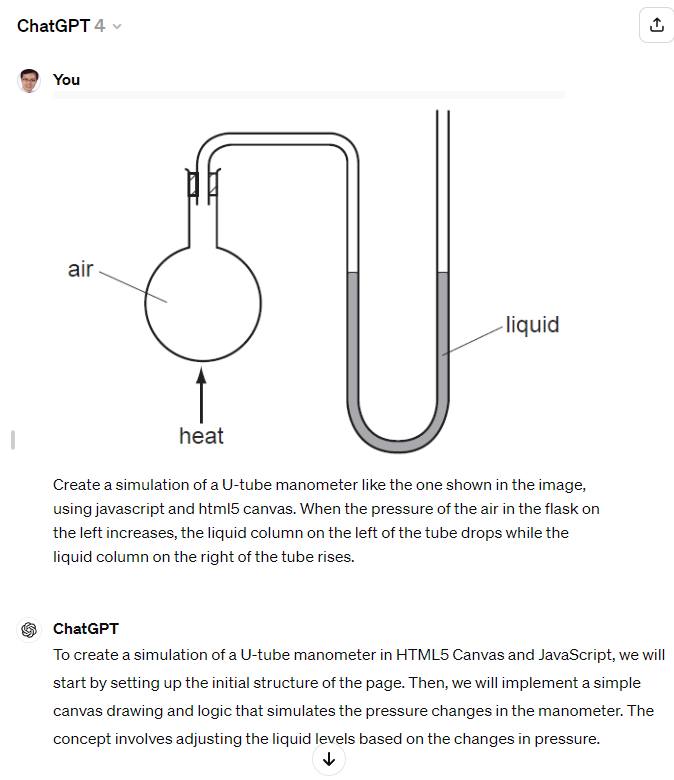
After trying to create a javascript simulation for the manometer using ChatGPT, I decided to return to GeoGebra, a platform that I am more used to, to create this interactive with more customisation. It comes with a ruler and a self-assessment feature for students to key in the value of pressure.
https://www.geogebra.org/m/qyuncz3h
A U-tube manometer is a fundamental device used to measure pressure differences in fluid systems with simplicity and precision. It consists of a U-shaped tube typically made from transparent glass or plastic, allowing for clear observation of fluid levels within the tube. The tube is partially filled with a manometric fluid such as mercury or water, chosen based on the expected pressure range and application. The manometer has a graduated scale for measuring the height difference between the fluid levels in the two arms of the U-tube. The device is connected at two points where the pressure difference needs to be assessed, such as in gas pipelines, liquid tanks, or other systems requiring pressure monitoring.
When the manometer is connected to the pressure sources, the fluid within the U-tube will adjust its levels until equilibrium is achieved, with one side rising and the other side falling. The difference in height between the two columns of fluid (h) indicates the pressure difference. This difference is read using the graduated scale and is used to calculate the pressure difference (ΔP) with the formula ΔP = ρgh, where ρ is the density of the manometric fluid, and g is the acceleration due to gravity.