After going through the topic of Dynamics in the A-level syllabus recently, it strikes me that there are several common mistakes or misconceptions that students whom I have taught over the years have always struggled with. I shall lay them out here in the hope that students who read this do not repeat the same mistakes.
1. Mixing up free-body diagrams involving multiple bodies in motion
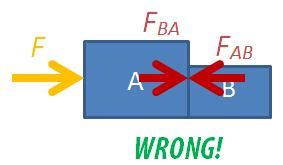
Students are often confused about the forces in drawing free-body diagrams, especially so when they have to consider the different parts of multiple bodies in motion. A common mistake that students make is to draw all the forces, including the internal forces within a system, on a single diagram.
To solve a two-body dynamics problems, students need to learn how to draw the 3 possible free-body diagrams. A detailed set of instructions is found in an earlier post.
2. Adding instead of subtracting momenta to find impulse
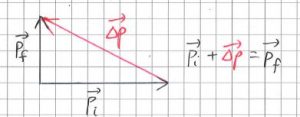
Students who do not have a strong foundation in Math may not appreciate the fact that the addition and subtracting of vectors is not done by simply adding or subtracting the magnitudes. Sometimes, students are asking to find the force acting on an object when given the initial and final momenta. The correct way to find the vector of the change in momentum is to place the tails of the initial and final momenta together, and to join the arrowhead of the initial momentum with that of the final momentum with a third vector in that direction.
They are often confused between finding the change in momentum and the act of adding two vectors together. When that happens, what teachers see is the following triangle instead.
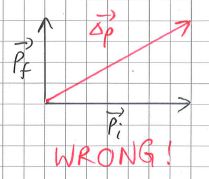
While the magnitude of the vector found in both diagrams are the same, students will get the wrong answer if asked for the direction of the change in momentum. This is actually an important notion because the direction of change in momentum is really the direction of the net force applied on the body.
3. Using wrong signs for momentum for head-on collisions
In A-level physics, in the study of collision problems, we will deal only with head-on collisions where two objects collide along the same line. Even then, students can get confused with the sign convention associated with the direction of motion of the objects.
Applying Conservation of Momentum
For a two body head-on collision problem, always start by writing down the following equation for the conservation of momentum:
[latex]m_Au_A +m_Bu_B = m_Av_A + m_Bv_B[/latex]
where [latex]m_X[/latex] is the mass of X, [latex]u_X[/latex] is the initial velocity of X, [latex]v_X[/latex] is the final velocity of X, where X is either A or B.
Follow this up by deciding on which direction you want to define as positive. For example, if you decide that the rightward direction is positive, the value of initial velocity for mass A is positive and that for mass B is negative.
What students sometimes do is to include the negative signs into the equation before substitution, e.g. [latex]m_Au_A +m_B(-u_B) = m_Av_A + m_Bv_B[/latex]. This causes confusion as they do not know where the directions of the final velocities are and hence, do not know which vectors to assign as negative.
What we should do instead is to determine the final direction of the velocities after we have found the values. Before we are able to do so, we shall assume that the final velocities are to the right. If the final value of velocity of a mass is negative, it means that its final velocity is to the left.
Substitute the values into equation.
Assuming that the initial speeds are both 4.0 m s-1;, the mass of A is 3.0 kg, mass of B is 5.0 kg, and that the collision is perfectly inelastic, we have:
[latex]3.0 \times 4.0+5.0 \times(-4.0)=(3.0+5.0) \times v[/latex]
[latex]-8.0=8.0v[/latex]
[latex]v=-1.0 \text{ m s}^{-1}[/latex]
This way, since the final velocity of the objects has a negative value, we can tell that the direction of the final velocity is to the left.