[accordions autoHeight=’true’]
[accordion title=”1. Work Done”]
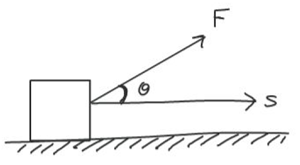
- Work done W is defined as the product of the force and the displacement made in the direction of the force.
- For a constant force F acting in same direction as the displacement s: W = F . s
- If $$\theta$$ is the angle between F and s: $$W = F\cos\theta\cdot s$$
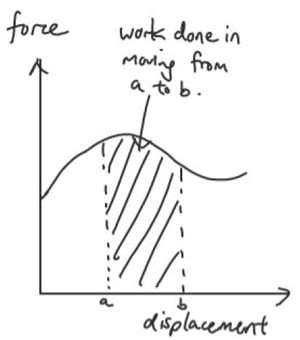
- Work done = Area under F-s graph.
[/accordion]
[accordion title=”1.1 Work Done on a Spring”]
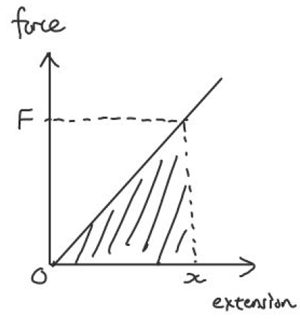
- Work done in stretching a spring = area under F-x graph = ½ Fx = ½ kx2
[/accordion]
[accordion title=”1.2 Work Done by a Gas”]
- Work done by expanding gas = area under P-V graph = $$\int P.dV$$
[/accordion]
[accordion title=”2. Kinetic Energy”]
- Kinetic energy is the energy of a body by virtue of its motion.
- Derive kinetic energy: W = F.s = ma.s = m ½(v2 – u2)
[/accordion]
[accordion title=”3. Potential Energy”]
- Potential energy is the energy of a body by virtue of it position.
- Gravitational Potential Energy near Earth’s surface: $$E_p = mgh$$
[/accordion]
[accordion title=”4. Conservation of Energy”]
- The Principle of Conservation of Energy states that energy can neither be created nor destroyed in any process. It can be transformed from one form to another, and transferred from one body to another but the total amount remains constant.
- The Work-Energy Theorem states that the net work done by external forces acting on a particle is equal to the change in mechanical energy of the particle. i.e. $$W=\Delta E_k+\Delta E_p$$
- Force $$F =-\dfrac{dU}{dx} = -\text{(gradient of Potential Energy vs displacement graph)}$$
[/accordion]
[accordion title=”5. Power”]
- Power is work done per unit time
- Instantaneous Power: $$P = \dfrac{dW}{dt} = F \dfrac{ds}{dt} = F v$$,
- Average Power: $$<P> = \dfrac{W}{t} = F <v>$$
[/accordion]
[accordion title=”6. Efficiency”]
- Efficiency $$\eta= \dfrac{E_{output}}{E_{input}}\times 100 \% \text{ or} \dfrac{P_{output}}{P_{input}}\times100\%$$
[/accordion]
[/accordions]