Seng Kwang Tan

08 August

Geiger–Müller counter simulation

Seng Kwang Tan AI, IP4 19 Nuclear Physics, Javascript, Simulations 0 Comments

A Geiger-Muller (GM) counter is an instrument for detecting and measuring ionizing radiation. It operates by using a Geiger-Muller tube filled with gas, which becomes ionized when radiation passes through it. This ionization produces an electrical pulse that is counted and displayed, allowing users to determine the presence and intensity of radiation.

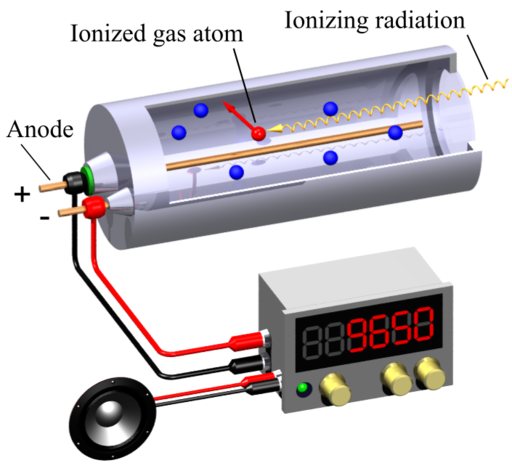
Svjo-2, CC BY-SA 3.0, via Wikimedia Commons

This simulation (find it at https://physicstjc.github.io/sls/gm-counter) allows students to explore the random nature of radiation and the significance of accounting for background radiation in experiments. Here’s a guide to help students investigate these concepts using the simulation.

Exploring Background Radiation

Q1: Set the source to “Background” and start the count. Observe the count for a few minutes. What do you notice about the counts recorded?

A1: The counts recorded are relatively low and vary randomly. This reflects the background radiation which is always present.


Q2: Why is it important to measure background radiation before testing other sources?

A2: Measuring background radiation is important to establish a baseline level of radiation. This helps in accurately identifying and quantifying the additional radiation from other sources.


Investigating a Banana as a Radiation Source

Q3: Change the source to “Banana” and reset the data. Start the count and observe the readings. How do the counts from the banana compare to the background radiation?

A3: The counts from the banana are higher than the background radiation. This is because bananas contain a small amount of radioactive potassium-40.


Q4: How do the counts per minute (CPM) for the banana vary over time? Is there a pattern or do the counts appear random?

A4: The counts per minute for the banana vary over time and appear random, reflecting the stochastic nature of radioactive decay.


Exploring a Cesium-137 Source

Q5: Set the source to “Cesium-137” and reset the data. Start the count and observe the readings. How do the counts from Cesium-137 compare to both the background radiation and the banana?

A5: The counts from Cesium-137 are significantly higher than both the background radiation and the banana. This is because Cesium-137 is a much stronger radioactive source.


Q6: What do the counts per minute (CPM) tell you about the intensity of the Cesium-137 source compared to the other sources?

A6: The CPM for Cesium-137 is much higher, indicating a higher intensity of radiation compared to the background and banana sources.


Understanding the Random Nature of Radiation

Q7: By looking at the sample counts, can you predict the next count value? Why or why not?

A7: No, you cannot predict the next count value because radioactive decay is a random process. Each decay event is independent of the previous ones.


Q8: How can you use the background radiation measurement to correct the readings from the banana and Cesium-137 sources?

A8: You can subtract the average background CPM from the CPM of the banana and Cesium-137 sources to get the corrected readings, isolating the radiation from the specific sources.


07 August

Graphical Representation of Waves

Seng Kwang Tan AI, Assessment, IP3 08 General Wave Properties 0 Comments

Use the quiz below to test your ability to interpret graphs of waves. You can click on a point in the map to read the values.

The codes for this quiz are generated by AI. However, the options and correct answers are rule-based and as such, should not have any errors.

It is able to randomly select from 4 different questions for displacement-distance graphs and 4 others for displacement-time graphs, while randomising the values of amplitude, wavelength and period.

05 August

East Zone Physics EdTech Workshop 6 Aug 2024

Seng Kwang Tan AI, Simulations 0 Comments

The hands-on workshop for Physics teachers will focus on the use of generative AI to create physics simulations without the user having to write code. The collection of the apps made using AI can be accessed here and the github repository here. This deck of slides is made available here for the participants’ reference. The sample prompts that we will be using can be found at the bottom of this page.

2024 EZ Physics Chapter EdTech Workshop AI-Generated Physics SimulationsDownload

The sample app that we hope the participants can produce will look something like this:

For your convenience, you may refer to the steps below.

STEP 1:

Open ChatGPT or any other GAI (e.g. Claude, CoPilot, Gemini)

STEP 2:

Copy these instructions and paste them into the AI.

  1. Put all the codes in one page.
  2. Create a canvas showing a ball dropped from rest from a height and bouncing off the ground using javascript.
  3. Using the plotly library, plot the graph of velocity versus time for the ball. The time of contact with the ground is negligible.​
  4. Create an input box that allows the user to key in the initial height in metres.​
  5. Create a slider that changes the percentage energy loss after every collision with the ground.
  6. Create a dropdown menu that changes the vertical axis to velocity or displacement.
  7. Initialise the animation and graph upon loading. Use a button to start and stop the animation.

STEP 3:

Copy the generated code using the button provided.

STEP 4:

Paste into editor here:


“Run in New Tab” to view and test the app. Download the html file once you are happy with it, or if you would like to add media objects such as images and audio.

STEP 5:

Be prepared to generate 10 or more versions! Repeat STEPS 3-4.

Debugging Options:

  1. Change the code manually yourself.
  2. Describe any unexpected behaviour / missing component to AI.
  3. Ask AI to try a new approach (usually after a few failed iterations).
  4. To save time, just ask AI to generate the codes that need to be changed. It will tell you where to update.

STEP 6:

Make the app look pretty!

  1. Optimise for SLS by asking AI to “limit the entire page to a size of max width 580px and max height: 460px”
  2. Ask AI to beautify the app with styling.
  3. Ask AI to add image / video / audio files into the code, giving it the filenames, e.g. replace the moving ball with an image of named “ball.png”. This is an example of such an image. You can right-click and “Save as” to save this image file into the same directory as the index.html file.

STEP 7:

To embed into SLS, you will need to copy the code libraries that are used (if any) in a new .js file. The code library is a collection of pre-written code that you can use to perform specific tasks, e.g.

  • plotly.js for continously changing graphs 
  • chart.js for static charts
  • papaparse.js for processing csv data

To make a copy of the file,

  1. Paste the link to the script on browser e.g. https://cdn.plot.ly/plotly-latest.min.js
  2. Save the page using the “Save as” option in the browser and place the file in the same directory as the html file.
  3. Rename the path to the file in this way:

STEP 8:

Download as HTML.
Save file as index.html. This is important for SLS packages as it will automatically load the index.html file by default.

STEP 9:

Zip all the files and upload the zip file into SLS component. Follow the user guide on how to do so: https://www.learning.moe.edu.sg/teacher-user-guide/author/html5-content-development/#uploading-a-html5-zip-file-in-sls

04 August

Interactive Graph with Javascript

Seng Kwang Tan 02 Kinematics, AI, IP3 02 Kinematics 0 Comments

I was experimenting with using generative AI to create an interactive graph that could be used to amend the animation of a moving particle, for the topic of kinematics. Students are able to move the four points on the velocity time graph to manipulate the movement. I kept the graph to straight lines between each point to keep things simple.

The vertical axis toggles between displacement and velocity. This will be yet another way for students to learn about how the velocity-time graph affects motion. I have found that many students are confused between displacement and velocity. The app’s ability for them to vary the velocity graph and then make predictions of the resulting displacement graph and the movement should be worth the effort.