Teaching Resources

Physics teaching resources

06 September

Pendulum-Powered Car

Seng Kwang Tan 03 Motion and Forces, 09 Oscillations, Lego 0 Comments

This pendulum-powered car is constructed using Lego Technic parts. I used mainly Lego beams to create the chassis and an “A” frame from which the pendulum is suspended. The pendulum is made of Lego beams and some wheels.

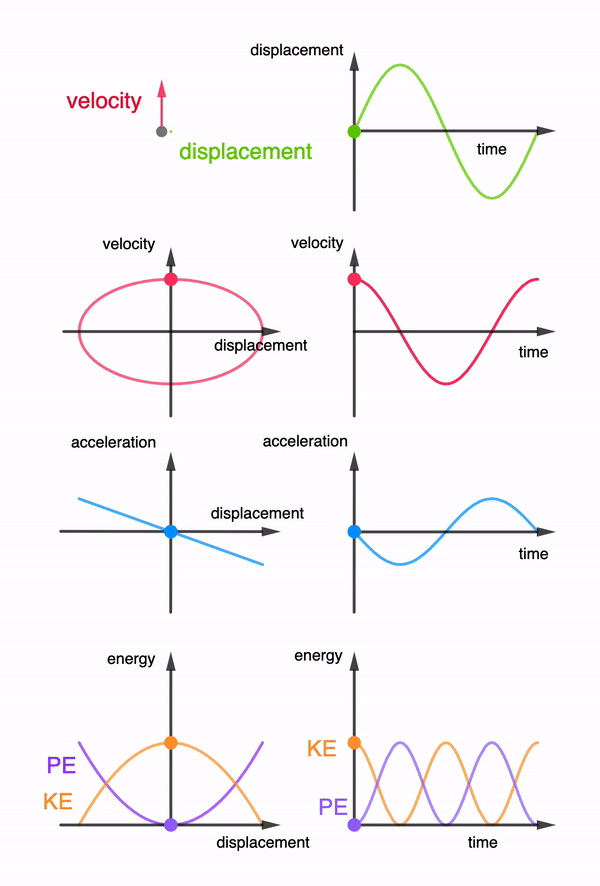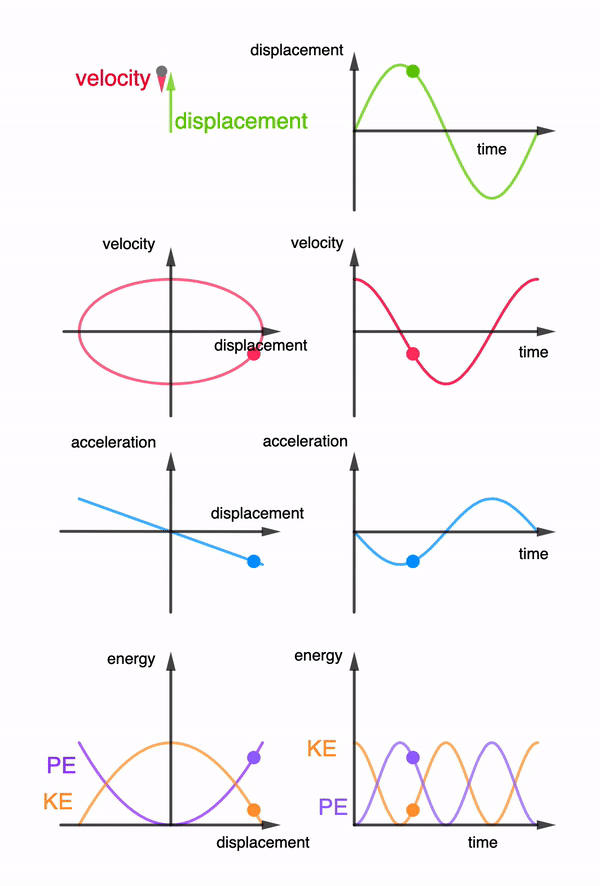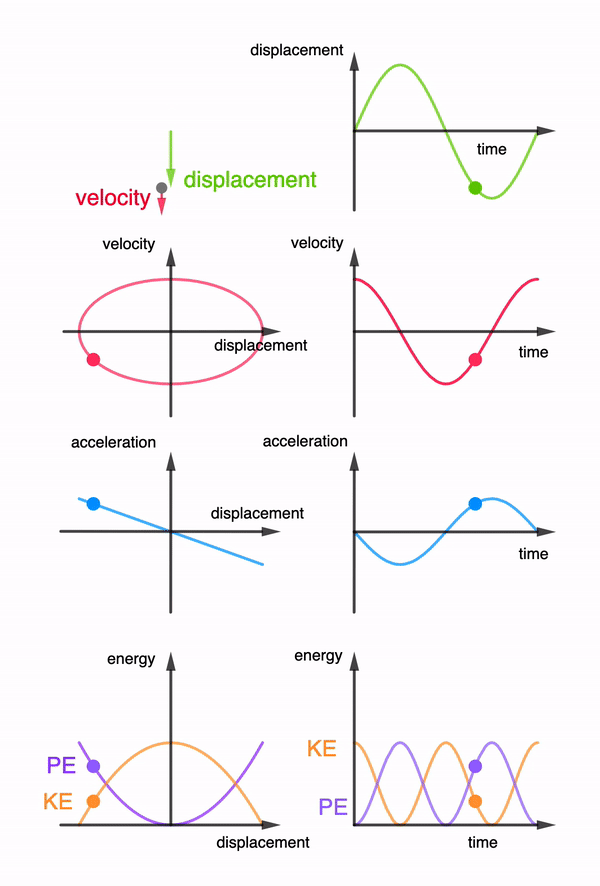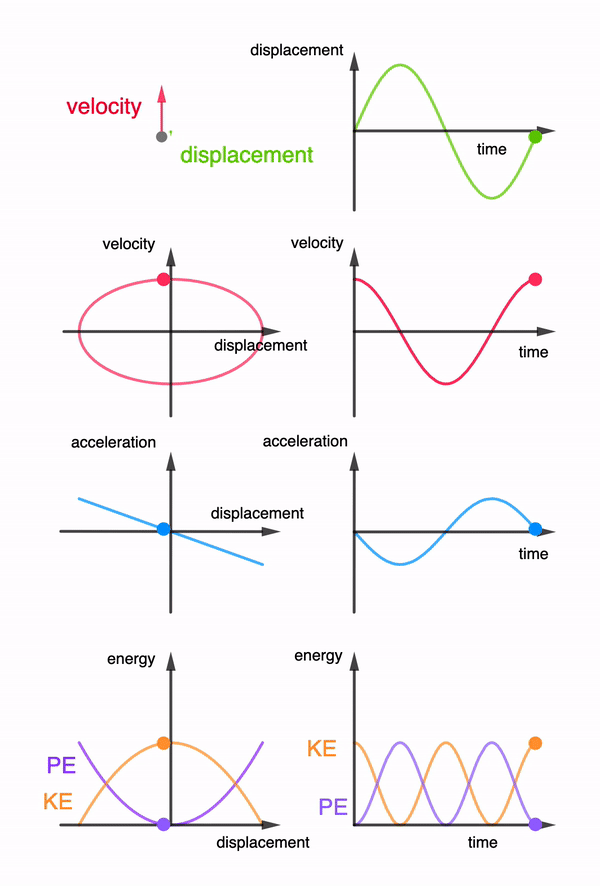
When the pendulum swings, it experiences an acceleration towards its equilibrium position. By the principle of conservation of momentum, the car experiences a change in momentum in the opposite direction. Since the acceleration of the pendulum changes its direction every half a cycle of its oscillation, the car will only oscillate about its original position if the wheels of the car are free to turn throughout the oscillation. 

A escapement mechanism which consists of a beam resting on a pair of 40-tooth gears attached to the front wheels prevent the wheels from rotating in the opposite direction. This means that the car will only be moving forward during the half of the pendulum’s oscillation when its displacement is at the front of its equilibrium position and pauses during the other half.

31 August

Simple harmonic motion graphs including energy

Seng Kwang Tan 09 Oscillations, GeoGebra 1 Comment

I have added two more graphs into the interactive animation. However, the app has become a bit sluggish when changing the period or amplitude. It still works smoothly when viewing the animation.

Students ought to find it useful to look at all the graphs together instead of in silo. This way, they can better understand the relationships between the graphs.

Here is an animated gif for use on powerpoint slides etc.

simple harmonic motion graphs
30 August

Simple Harmonic Motion Graphs

Seng Kwang Tan 09 Oscillations, GeoGebra 0 Comments

Here’s my attempt at animating 5 graphs for simple harmonic motion together in one page.

From left column:

$$v = \pm\omega\sqrt{x_o^2-x^2}$$

$$a = -\omega^2x$$

From right column:

$$s = x_o\sin(\omega t)$$

$$v = x_o\omega \cos(\omega t)$$

$$a = -x_o\omega^2 \sin(\omega t)$$

And here is the animated gif file for powerpoint users:

Simple harmonic motion graphs - displacement-, velocity-, acceleration- time graphs and more
26 August

Phase Difference

Seng Kwang Tan 10 Wave Motion, GeoGebra 4 Comments

The first of two apps on Phase Difference allows for interaction to demonstrate the oscillation of two different particles along the same wave with a variable phase difference.

The second shows two waves also with a phase difference.

In both cases, the phase difference $\Delta\phi$ can be calculated with

$$\Delta\phi = \dfrac{\Delta x}{\lambda} \times 2\pi$$

where $\Delta x$ is the horizontal distance between the two particles or the horizontal distance between the two adjacent identical particles (one from each wave) and $\lambda$ is the wavelength of the waves.

25 August

Longitudinal and Transverse Waves

Seng Kwang Tan 10 Wave Motion, GeoGebra, IP3 08 General Wave Properties 0 Comments

I modified Tom Walsh’s original GeoGebra app to add a moveable single oscillating particle for students to observe its movement along a longitudinal wave and a transverse wave.

The app can also be used to show how the displacement of a particle in a longitudinal wave can be mapped onto a sinusoidal function, similar to the shape of a transverse wave. For example. a displacement of the particle to the right can be represented by a positive displacement value on the displacement-distance graph.

You can choose to select the particle that you want to focus on by using the slider.

For a full screen view, visit https://www.geogebra.org/m/auyft2pd

Here is an animated gif for those who prefer to insert it into a powerpoint slideshow instead:

Animation of longitudinal wave and transverse wave

For embedding into SLS or any platform that supports iframes.

<iframe scrolling="no" title="Progressive Waves" src="https://www.geogebra.org/material/iframe/id/auyft2pd/width/640/height/480/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/false/ctl/false" width="640px" height="480px" style="border:0px;"> </iframe>