The simulation serves to show how the magnetic field of one current-carrying wire exerts a force on another current-carrying wire.
When two wires are placed parallel to each other and carry electric currents, each wire produces its own magnetic field. The magnetic field around a straight current-carrying conductor forms concentric circles, and the direction of these circles can be determined by the right-hand grip rule: if you point your thumb along the direction of the current, your curled fingers show the direction of the magnetic field lines.
Because of this, one wire is always sitting inside the magnetic field created by the other. The moving charges in the second wire—that is, the current—interact with this magnetic field and experience a force. The strength of the force depends on the current in both wires and the distance between them, while the direction of the force can be worked out using Fleming’s left-hand rule or simply by considering how the two fields interact.
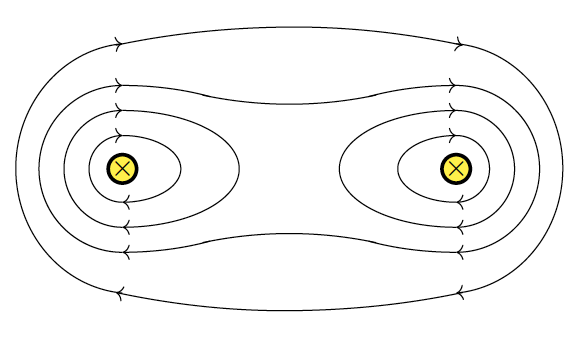
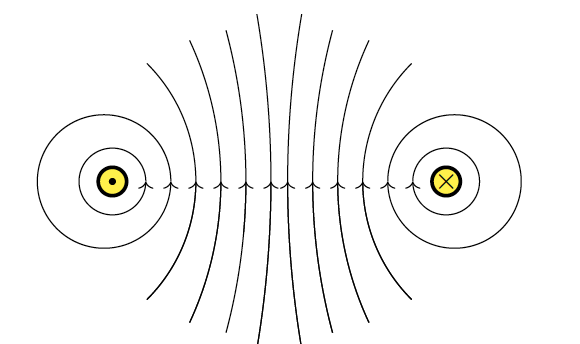
Magnetic field patterns between two parallel currents interact in such a way as to form either an attraction (for currents in same direction) or a repulsion (for opposite currents)
If the currents in the two wires flow in the same direction, the magnetic fields between the wires reinforce each other, producing a stronger field outside the pair and a weaker field between them. This imbalance pulls the wires towards each other, so they attract. On the other hand, if the currents run in opposite directions, the magnetic fields between the wires reinforce instead, while the fields outside are weakened. The result is a pushing apart of the two wires, so they repel each other.
In short, the force on parallel wires arises because each wire generates a magnetic field that acts on the current in the other. Identifying the force is straightforward once you know the directions of the currents: currents in the same direction cause attraction, while currents in opposite directions cause repulsion.
