16 September

A dynamics problem – apparent weight

Seng Kwang Tan IP3 03 Dynamics 0 Comments

This is a problem posed by a student today:

A boy of mass 40 kg is standing on a weighing machine inside a lift which is moving upwards. At a certain moment, the speed of the lift is $3.0 \text{ m s}^{-1}$ and it is decelerating at $2.0 \text{ m s}^{-2}$. What is the reading (in kg) shown on the weighing scale?

My advice for any dynamics problem is to take the direction of acceleration as positive. This way, you can apply Newton’s second law directly without worrying about inserting extra negative signs for deceleration. After all, a negative value of acceleration simply comes from the chosen sign convention—it reflects direction. For simplicity, putting the direction of acceleration as positive (in this case, downward is positive), we have

$$F_{net} = ma$$

The net force should therefore, be $W – N$, where $N$ is smaller than $W$.

$$W – N = ma$$

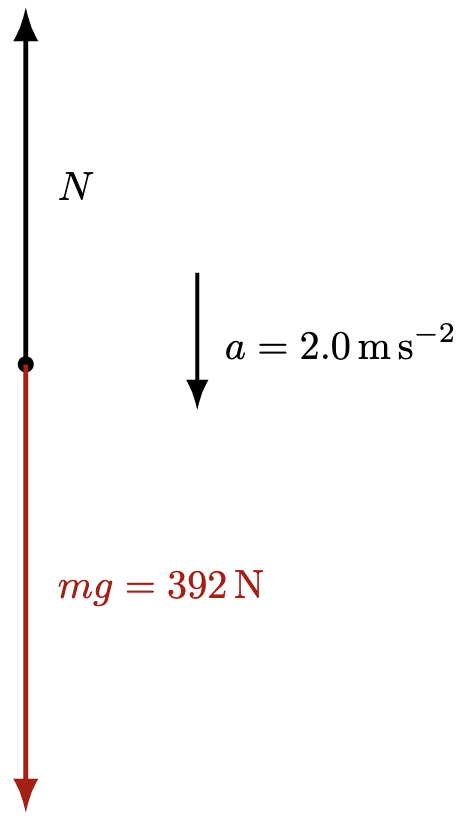
Substituting, we have

$$mg – N = ma$$

$$(40 \text{ kg} \times 9.81 \text{ N kg}^{-1}) – N = 40 \text{ kg} \times 2.0 \text{ m s}^{-2}$$

$$N = 312 \text{ N}$$

Note that $N$ is also known as apparent weight.

The mass reading due to this normal force = $\dfrac{312\text{ N}}{9.81 \text{ N kg}^{-1}} = 32 \text{ kg}$

(Notice here that the speed of the lift is irrelevant.)

The GeoGebra simulation allows you to modify the acceleration and observe the change in the vector representing the normal contact force, which is force acting on the weighing scale.

Open in new tab 🔗

For a real-life experiment along with a visualisation of the changes in the vectors based on this scenario, check out my video and simulation.

14 September

Kinematics Equations – which to use?

Seng Kwang Tan IP3 02 Kinematics 0 Comments
Open in new tab 🔗

When tackling kinematics problems, a quick way to decide which equation to use is to look carefully at which variables are given and which one you need to find. The four equations involve only five quantities — $u$ (initial velocity), $v$ (final velocity), $a$ (acceleration), $t$ (time), and $s$(displacement). Each equation links four of them, leaving one out. So if, for example, time $t$ is not mentioned anywhere in the problem, the best choice is usually the equation $v^2 = u^2 + 2as$, since that one does not involve $t$. By matching the known and unknown quantities against the “missing variable” in each equation, you can quickly narrow down the correct equation to apply.

13 September

Electrostatic Precipitator Simulation

Seng Kwang Tan IP4 10 Static Electricity 0 Comments
Open in new tab 🔗

Interact with the simulation of an electrostatic precipitator (ESP) above. The ESP is a big air cleaner for factories and power plants. It uses electricity to pull tiny dust and mist out of smoky gas before the gas goes up the stack. Inside the box are thin wires kept at a very high voltage next to large metal plates that are grounded. The high voltage makes a faint “corona” around the wires, which is a cloud of charged ions. As the dirty gas flows past, those ions bump into the dust particles and give them an electric charge, kind of like when a balloon rubs on your sweater and becomes “static.”

Once the particles are charged, the electric field pushes them sideways toward the plates. Positive particles are pulled one way, negative the other, but either way they end up sticking to a plate instead of staying in the air stream. The cleaned gas keeps moving forward and exits the ESP. Every so often, the plates are cleaned: in a dry ESP, mechanical “rappers” gently shake the plates so the dust falls into hoppers; in a wet ESP, water rinses the plates so sticky mist and very fine droplets wash off.

ESP performance depends on keeping the electric field strong and the gas flow smooth, and on the dust being “just right” electrically—if it holds charge too well or not well enough, efficiency drops. When everything is tuned properly, an ESP can remove well over 99% of particles with very little resistance to airflow. That’s why they’re widely used to protect the air around power plants, cement kilns, and other heavy industries.

11 September

RC Circuit

Seng Kwang Tan 16 Circuits, GeoGebra 0 Comments
Open in new tab 🔗

This is meant for the A-level topic of Circuits, for which students have to describe and represent the variation with time, of quantities like current, charge and potential difference, for a capacitor that is charging or discharging through a resistor, using equations of the form $x = x_0e^{-\frac{t}{\tau}}$ or $x = x_0(1 – e^{-\frac{t}{\tau}})$, where $\tau = RC$ is the time constant.

This GeoGebra interactive by Dave Nero is well-designed. It illustrates how the charge, voltage, and current in an RC circuit change over time. You can adjust the resistance, capacitance, and supply voltage using the sliders provided. The two circuit switches can be opened or closed by selecting the check boxes. A drop-down menu allows you to choose which quantity to display on the graph, and pressing the play button in the lower left corner starts the time-dependent plot.

When a capacitor is connected in series with a resistor, the changes in current, charge and potential difference follow an exponential pattern, controlled by the time constant $\tau = RC$.

During charging, the capacitor begins with no charge, so the battery’s full potential difference appears across the resistor, giving a maximum initial current. As charge accumulates on the plates, the potential difference across the capacitor rises. This reduces the potential difference across the resistor, causing the current to decrease. The charge on the capacitor and its potential difference both increase with time according to the equation $x = x_0 \left(1 – e^{-t/\tau}\right)$, approaching their maximum values asymptotically. Meanwhile, the current decreases exponentially with time, following $x = x_0 e^{-t/\tau}$.

During discharging, the capacitor starts with an initial charge and potential difference. Once connected across the resistor, this stored energy drives a current in the circuit. As the charge leaves the plates, the potential difference across the capacitor falls. Both charge and potential difference decrease exponentially with time according to $x = x_0 e^{-t/\tau}$, and the current also decays exponentially to zero, reversing direction compared to charging.

The time constant $\tau = RC$ sets the rate of change. After one time constant, a charging capacitor reaches about 63% of its final charge, or a discharging capacitor falls to about 37% of its initial charge. After about five time constants, the process is practically complete.

11 September

Bouncing ball with energy loss

Seng Kwang Tan 03 Motion and Forces, AI, IP3 02 Kinematics, IP3 03 Dynamics, IP3 06 Work, Energy and Power, Simulations 0 Comments
Open in new tab 🔗

This simulation offers a clear and interactive way to explore the motion of a ball bouncing on the ground, highlighting how displacement, velocity, and acceleration change over time. On the left, you’ll see the animation of the ball with vectors showing its position (green), velocity (pink), and acceleration (blue). The sliders at the top allow you to adjust the starting height, the percentage of energy lost on each bounce, and whether air resistance is included. You can pause, reset, or let the motion run continuously, while the time slider doubles as a scrubber when the simulation is paused.

On the right, the three graphs display how each physical quantity varies with time. The position–time graph shows the ball’s vertical displacement, always measured relative to the lowest point of its center of mass. The velocity–time graph alternates between negative and positive values, reflecting the downward and upward motion during each bounce, while the acceleration–time graph remains mostly constant at –g, with spikes at the moment of collision. Together, the animation and graphs help link the visual motion with the quantitative data, reinforcing the relationships between these variables.

The underlying theory follows Newton’s laws of motion. The ball accelerates downwards under gravity until it collides with the ground, where it loses some energy depending on the restitution factor. This is why the bounce height diminishes over time. The velocity vector shows not only the speed but also the direction of motion, while the acceleration vector indicates that gravity always acts downward, regardless of whether the ball is rising or falling. By adjusting energy loss during each collision and air resistance, you can model more realistic scenarios and see how dissipative forces affect motion, making this a powerful tool to visualize the physics of bouncing objects.

11 September

Dropping with air resistance

Seng Kwang Tan 03 Motion and Forces, IP3 02 Kinematics, Javascript 0 Comments
Open in new tab 🔗

This simulation lets you watch two equal-size spheres (light and heavy) fall, while you see their free-body diagrams (FBDs) and a velocity–time graph update in real time.

Press Start to run and Pause to discuss a moment in time. Reset restarts from rest. Use Zoom to read the force vectors clearly. Toggle Air Resistance to compare an idealised fall (no drag) with a more realistic one (drag on). The small info panel shows the current speeds and, when drag is on, each sphere’s terminal velocity.

What to look for

  • Without air resistance: Each FBD shows only weight downward. Acceleration is constant at ggg, so the velocity–time graph is a straight line from the origin for both spheres (same slope, because mass doesn’t matter when no drag acts).
  • With air resistance: A drag arrow appears upward and grows with speed. The heavy sphere’s velocity rises faster at first (its weight is larger), but both curves flatten as drag increases, and the acceleration vector shrinks toward zero. Dotted segments indicate when the two curves overlap closely.

Theory in one breath

In air, we model drag as proportional to speed: $F_\text{drag}=kv$

Net force is $ma=mg−kv \quad\Rightarrow a=g−\dfrac{k}{m}v$

As v grows, the term $\dfrac{k}{m}v$ eats into $g$, so acceleration falls.

Terminal velocity happens when forces balance: $mg=kv$​, so $v_t=\dfrac{mg}{k}$

Heavier mass ⇒ larger $v_t$​. That’s why the heavy sphere ultimately settles at a higher speed and takes longer to level off. With drag off, the model is simply $a=g$ and $v=gt$.

How to teach with it (fast)

  1. Start with Air Resistance off: Pause after a second—ask why both lines match and why only weight appears on the FBDs.
  2. Turn Air Resistance on: Run, then pause midway. What changed in the FBDs? Why is acceleration smaller now?
  3. Let it run until the acceleration vectors nearly vanish: connect “flat graph” with “balanced forces,” then read off different terminal velocities.

That’s it: start, pause, notice which vector changed, and link the picture to the equation.