16 Circuits

11 September

RC Circuit

Seng Kwang Tan 16 Circuits, GeoGebra 0 Comments
Open in new tab 🔗

This is meant for the A-level topic of Circuits, for which students have to describe and represent the variation with time, of quantities like current, charge and potential difference, for a capacitor that is charging or discharging through a resistor, using equations of the form $x = x_0e^{-\frac{t}{\tau}}$ or $x = x_0(1 – e^{-\frac{t}{\tau}})$, where $\tau = RC$ is the time constant.

This GeoGebra interactive by Dave Nero is well-designed. It illustrates how the charge, voltage, and current in an RC circuit change over time. You can adjust the resistance, capacitance, and supply voltage using the sliders provided. The two circuit switches can be opened or closed by selecting the check boxes. A drop-down menu allows you to choose which quantity to display on the graph, and pressing the play button in the lower left corner starts the time-dependent plot.

When a capacitor is connected in series with a resistor, the changes in current, charge and potential difference follow an exponential pattern, controlled by the time constant $\tau = RC$.

During charging, the capacitor begins with no charge, so the battery’s full potential difference appears across the resistor, giving a maximum initial current. As charge accumulates on the plates, the potential difference across the capacitor rises. This reduces the potential difference across the resistor, causing the current to decrease. The charge on the capacitor and its potential difference both increase with time according to the equation $x = x_0 \left(1 – e^{-t/\tau}\right)$, approaching their maximum values asymptotically. Meanwhile, the current decreases exponentially with time, following $x = x_0 e^{-t/\tau}$.

During discharging, the capacitor starts with an initial charge and potential difference. Once connected across the resistor, this stored energy drives a current in the circuit. As the charge leaves the plates, the potential difference across the capacitor falls. Both charge and potential difference decrease exponentially with time according to $x = x_0 e^{-t/\tau}$, and the current also decays exponentially to zero, reversing direction compared to charging.

The time constant $\tau = RC$ sets the rate of change. After one time constant, a charging capacitor reaches about 63% of its final charge, or a discharging capacitor falls to about 37% of its initial charge. After about five time constants, the process is practically complete.

18 February

Delight – a web-based board game on electricity

Seng Kwang Tan 16 Circuits, Games, IP4 12 DC Circuits, Javascript 0 Comments

I had previously shared about this physical board game that I designed to teach electricity concepts. Now, with ChatGPT’s help, I have managed to produce a simple implementation of the board game so that there is no need to print and cut out the pieces anymore.

However, the game is still unable to detect if the light bulb will light up and automatically change the image colour or add the scores. That will require further complex programming due to the many possible outcomes for this game.

https://physicstjc.github.io/sls/delight/index.html

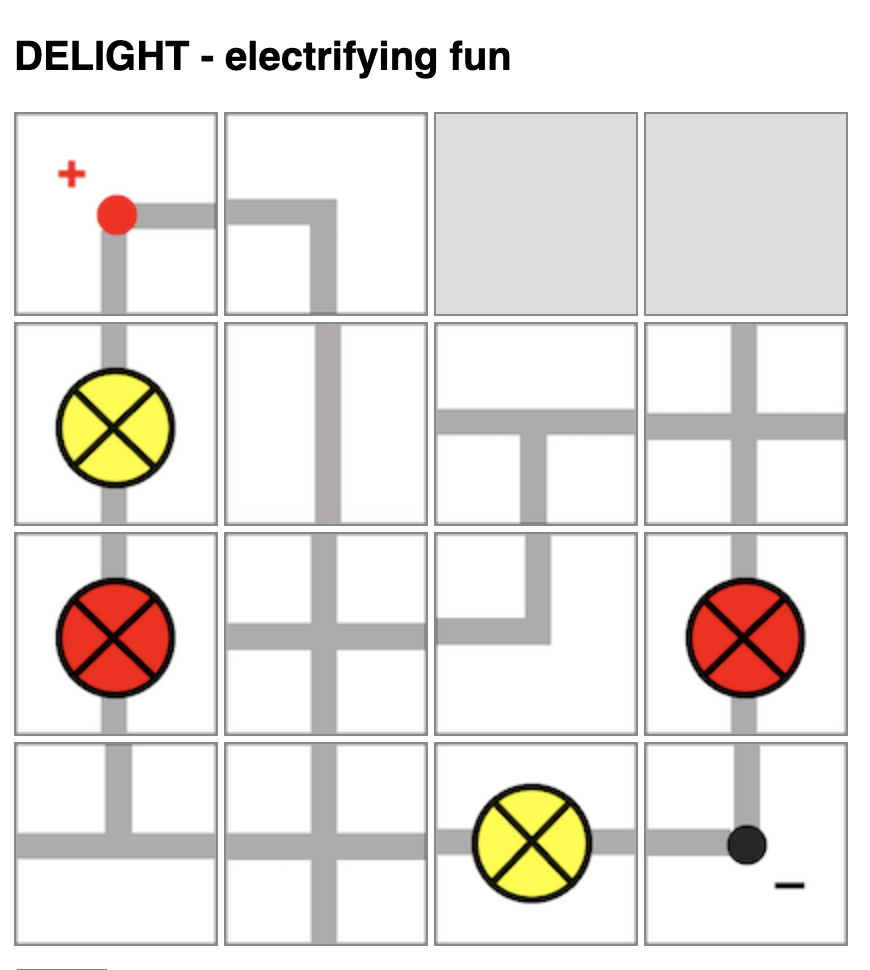
The rules of the game are as such:

  1. Players will take turns to connect their own bulbs to the terminals while trying to sabotage their opponent’s bulbs.
  2. Players will take turns to place one piece on the 4-by-4 game board by clicking to select the electrical component and clicking on the square on the board to place it.
  3. Upon placing the piece, the player can also turn that piece in any orientation (by clicking on it) within the same turn.
  4. Players can choose to use up to two turns at any point in the game to rotate any piece that had been placed by any player.
  5. In other words, each player has 9 turns: 7 placement turns and 2 rotation turns.

At lower levels, students can compete to see who has the most lit bulbs. However, they will need to be able to identify which light bulbs are lit. Do watch out for short-circuits.

At higher levels, students can compete to see whose light bulbs has the most total electrical power, with some calculations involved.

02 April

Internal Resistance and Terminal Potential Difference

Seng Kwang Tan 16 Circuits, GeoGebra, IP4 12 DC Circuits 0 Comments

https://www.geogebra.org/m/puvfjxk5

This applet demonstrates how terminal potential difference (as measured by the voltmeter across the terminals of the battery) changes depending on :

  1. internal resistance r
  2. external resistance R
  3. emf E
  4. when a switch is turned on and off
<iframe scrolling="no" title="Internal Resistance and Terminal Potential Difference" src="https://www.geogebra.org/material/iframe/id/puvfjxk5/width/640/height/480/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="640px" height="480px" style="border:0px;"> </iframe>
28 March

Potential Divider with Thermistor Applet

Seng Kwang Tan 16 Circuits, GeoGebra, IP4 12 DC Circuits 0 Comments

The wonderful thing about GeoGebra is that you can whip up an applet from scratch within an hour just before your lesson and use it immediately to demonstrate a concept involving interdependent variables. I was motivated to do this after trying to explain a question to my IP4 students.

The RGB colours of the thermistor reflects the temperature (red being hot, bluish-purple being cold)

https://www.geogebra.org/m/etszj23m

This was done to demonstrate the application of potential dividers involving a thermistor and a variable resistor. It can, of course, be modified very quickly to introduce other circuit components.

23 September

Geogebra App on Maximum Power Theorem

Seng Kwang Tan 16 Circuits, GeoGebra 0 Comments

GeoGebra link: https://www.geogebra.org/m/hscshcj8

This simulation demonstrates the power dissipated in a variable resistor given that the battery has an internal resistance (made variable in this app as well).

Since the power dissipated by the resistor is given by

[latex]P=I^2R[/latex]

and the current is given by

[latex]I=E(R+r)[/latex],

[latex]P=E^2\times\dfrac{R}{(R+r)^2}=\dfrac{E^2}{\dfrac{r^2}{R}+R+2r}[/latex]

This power will be a maximum if the expression for the denominator [latex]\dfrac{r^2}{R}+R+2r[/latex] is a minimum.

Differentiating the expression with respect to R, we get
[latex]\dfrac{d(\dfrac{r^2}{R}+R+2r)}{dR}=-\dfrac{r^2}{R^2}+1[/latex]

When the denominator is a minimum,
[latex]-\dfrac{r^2}{R^2}+1=0[/latex]

Therefore,
[latex]r=R[/latex] when the power dissipated by the resistor is highest.

22 September

Geogebra Simulation of a Potentiometer

Seng Kwang Tan 16 Circuits, GeoGebra, Simulations 0 Comments

Some of the more challenging problems in the topic of electricity in the A-level syllabus are those involving a potentiometer. The solution involves the concept of potential divider and the setup can be used to measure emf or potential difference across a variety of circuits components. Basically, students need to understand the rule – that the potential difference across a device is simply a fraction of the circuit’s emf, and that fraction is equal to the resistance of the device over the total resistance of the circuit.

[latex]V_{device}=\frac{R_{device}}{R_{total}}*emf[/latex]

The intention of this Geogebra app is for students to practise working on their calculations, as well as to reinforce their understanding of the principle by which the potentiometer works.

GeoGebra link: https://www.geogebra.org/m/pzy3qua8