The following is a question (of a more challenging nature) posed to JC1 students when they are studying the topic of kinematics.
A gun is aimed in such a way that the initial direction of the velocity of its bullet lies along a straight line that points toward a coconut on a tree. When the gun is fired, a monkey in the tree drops the coconut simultaneously. Neglecting air resistance, will the bullet hit the coconut?
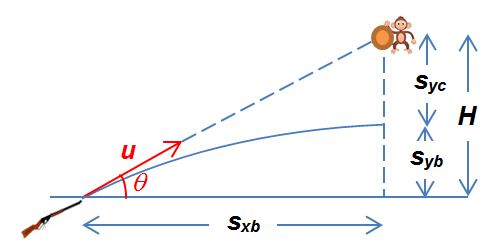
It is probably safe to say that if the bullet hits the coconut, the sum of the downward displacement of coconut $$s_{yc}$$ and the upward displacement of the bullet $$s_{yb}$$ must be equal to the initial vertical separation between them, i.e. $$s_{yc}+s_{yb}=H$$
This is what we need to prove.
Since $$s_{yc}=\frac{1}{2}gt^2$$
$$s_{yb}=u\text{sin}\theta{t}-\frac{1}{2}gt^2$$ and $$s_{xb}=u\text{cos}\theta t$$
$$s_{yc}+s_{yb}=u\text{sin}\theta{t}=u\text{sin}\theta\times \frac{s_{xb}}{u\text{cos}\theta}=s_{xb}\times{\text{tan}\theta}$$
At the same time, the relationship between $$H$$ and the horizontal displacement of the bullet $$s_{xb}$$ before it reaches the same horizontal position of the coconut is $$\text{tan}\theta=\frac{H}{s_{xb}}$$
Hence, $$s_{yc}+s_{yb}=H$$