For my students: To download the file and video for analysis using Tracker, right-click the file here…
To verify the equation F = ma, where F is the resultant force on an object, m is the mass of the object and a is the acceleration, this is one of the ways to do so:
Equipment:
1. Motion Sensor
2. Datalogger
3. Cart with variable mass
4. End Stop
5. Pulley with clamp
6. Hanger Mass Set
7. String (about 1.2 m)
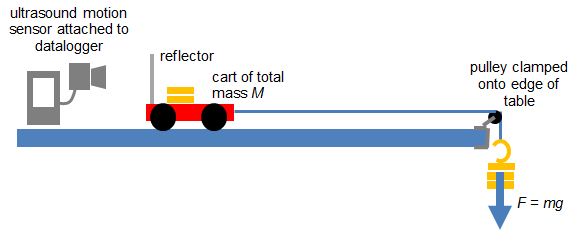
For a system of a cart of mass M on a horizontal track that is connected to a hanging mass m with a string over a pulley, the net force F on the entire system (cart and hanging mass) is the weight of hanging mass. F = mg (no friction assumed).
According to Newton’s Second Law, mg = (M+ m)a. We will try to prove experimentally that this is true in the video below.